Background
Connected Autonomous Vehicles (CAVs) are expected to enable reliable and efficient transportation systems. Most cooperative driving approaches for CAVs and motion planning algorithms for multi-agent systems are not completely safe because they implicitly assume that all vehicles/agents will execute the expected plan within a small margin of error. This assumption, however, may not always be valid since CAVs may have to slow down (e.g., to yield to a jaywalker) or be forced to stop (e.g., in a breakdown event), sometimes without notice. Responsibility-Sensitive Safety (RSS) defines a set of safety rules for each driving scenario to ensure that a vehicle will not cause an accident irrespective of other vehicles' behavior. Despite RSS development efforts, rules can fall short of effectively covering many scenarios such as merges, intersections, unstructured roads, and deadlock situations.
Invention Description
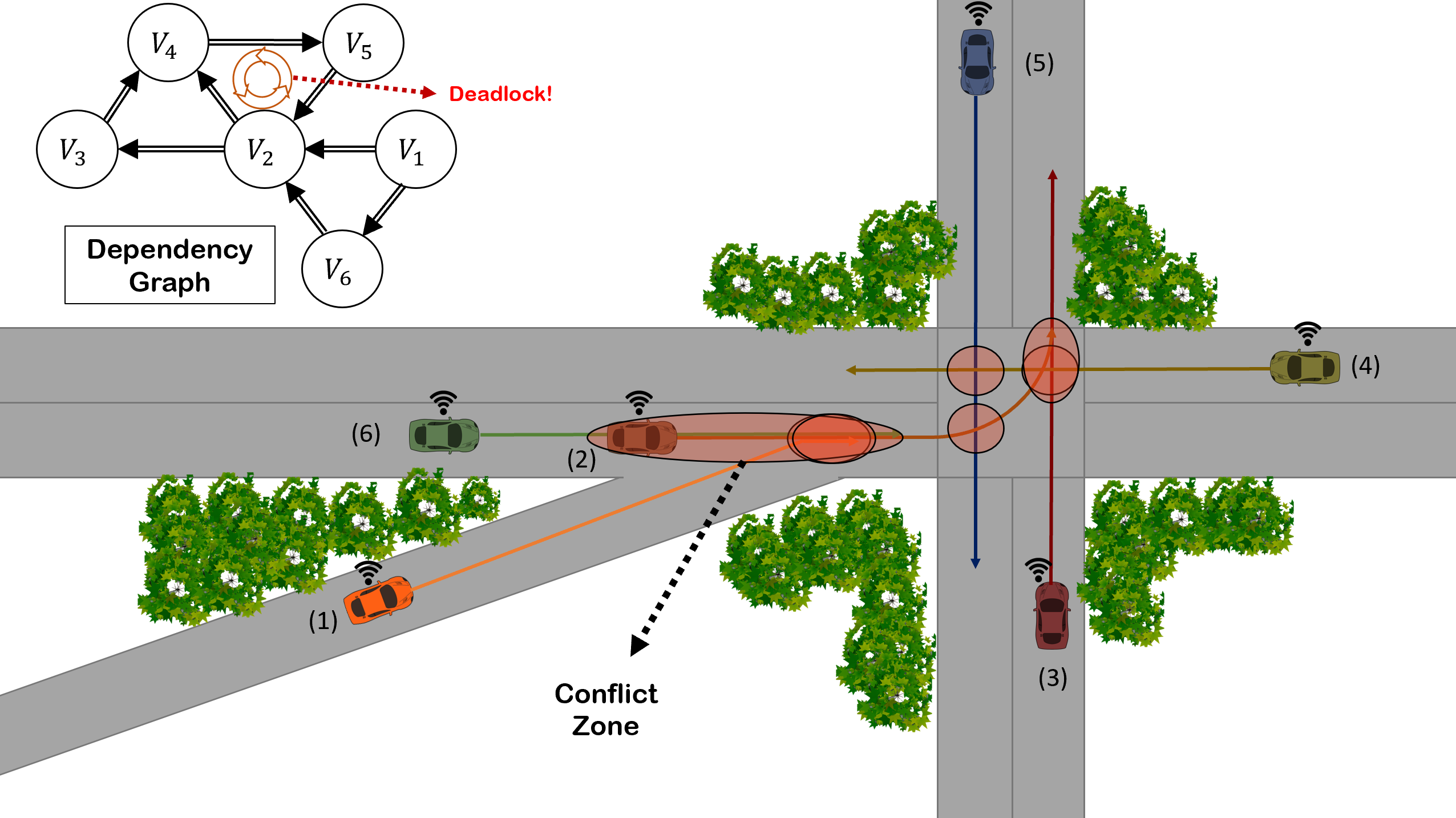
Researchers at Arizona State University have developed a cooperative driving and deadlock resolution approach for CAVs. Instead of a lane-based coordinate system, future trajectories of CAVs are used to represent their conflicts, which can be applied to any road geometries and situations. Inspired by the RSS legal/blame perspective, a new set of safety rules for CAVs were developed to guarantee that no accidents happen if CAVs abide by proposed RSS rules. An efficient decentralized deadlock detection and resolution algorithm for CAVs is also a critical part of this work. Results from simulation experiments—which consider vehicle dynamics and network delays—demonstrate that all CAVs remain safe even if one or more CAVs slow down or stop at any point in time.
Potential Applications
• Connected autonomous vehicles
• Smart cities
• Autonomous mobile robots in warehouses
Related Publication: Cooperative Driving of Connected Autonomous Vehicles Using Responsibility-Sensitive Safety (RSS) Rules